Batch Normalization
Problem Statement
The inputs to each layer of a neural network have corresponding distributions, and during training, the change in parameters of the previous layers has an impact on these distributions. This variation slows down training by requiring lower learning rates and careful parameter initialization, and it makes training models with saturating nonlinearities very difficult. The effect of the randomness on the distribution of the inputs to internal layers during training due to the change in network parameters is known as internal covariate shift. This problem of internal covariate shift is addressed by Batch Normalization.
Batch normalization (also known as the batch norm) is a technique for making artificial neural network training faster and more stable by normalizing the layers’ inputs for each training mini-batch. This normalization reduces the effect of internal covariate shift, allowing for faster training with higher learning rates. It achieves the same accuracy with 14 times fewer training steps and significantly outperforms the original model.

To summarize, the following are some of the benefits of using batch normalization in neural networks:
- It allows for faster learning rates and the training of deep networks by reducing internal covariate shifts.
- It simplifies the hyperparameter search problem and adds more flexibility for parameter initialization.
- It slightly regularizes the model by adding a small amount of noise during normalization.
Current Approach
During training, batch normalization attempts to normalize a batch of inputs to each layer before they are fed to the non-linear activation unit. As a result, the input to the activation function of each next layer in each training batch has a mean of 0 and a variance of 1. This mean and variance can be shifted and scaled by two learnable parameters α and β.

Experimentation Setup
To test the effect of internal covariance shift on training and to demonstrate the capability of Batch Normalization, MNIST and ImageNet datasets were used in the paper [1].
MNIST dataset
The MNIST dataset is widely used in computer vision and deep learning. It contains 60,000 small square 2828-pixel grayscale images of handwritten single digits ranging from 0 to 9. Since the data set is already in standard form, no additional preprocessing is necessary.
The architecture consists of three fully connected hidden layers, each with 100 activations. Each hidden layer has a sigmoid activation function and weights that are initialized to small random Gaussian values. The final layer is a fully connected layer with 10 activations and a loss function of cross-entropy loss. The network was trained for 50K steps with 60 examples per mini-batch, and baseline and batch-normalized networks were compared.
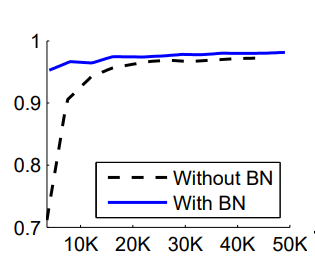
The graph clearly shows that Batch Normalization enables the network to train faster and with greater accuracy. It is because, as training progresses, the distributions in the batch-normalized network become much more stable, which aids in training.
ImageNet dataset
The ImageNet is a large visual database that is organized in the WordNet hierarchy. Its WordNet contains over 100,000 synsets, each with an average of 1000 images to illustrate it.
Batch Normalization was applied to a new variant of the Inception network that had been trained on the ImageNet classification task. The network contains many convolutional and pooling layers, as well as a softmax layer that predicts the image class out of 1000 possibilities. Along with batch normalization, the following modifications were done to achieve the maximum benefit:
- Increase learning rate
- remove dropout
- reduce L2 weight regularization
- Accelerate the learning rate decay, and so on.
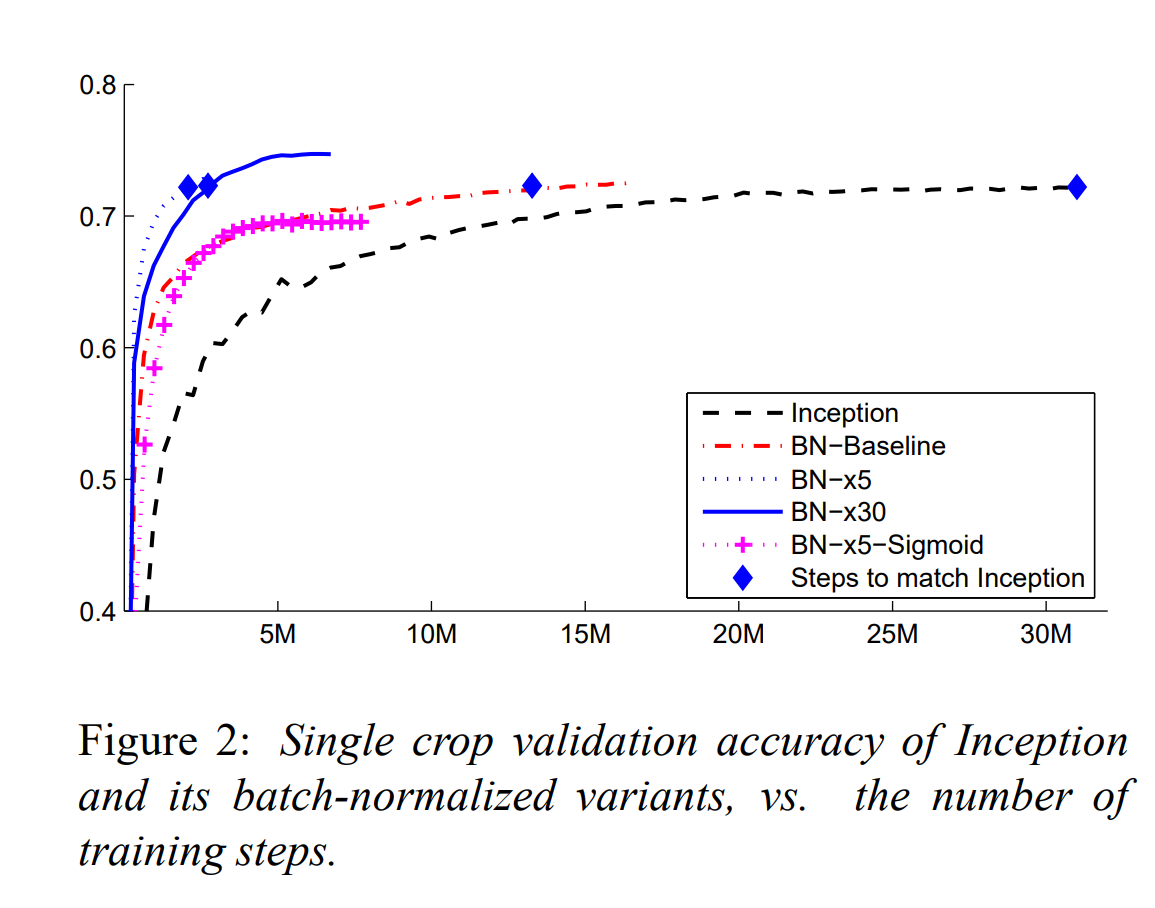
The accuracy of Inception was achieved in less than half the number of training steps by only using Batch Normalization (BN-Baseline). Further tweaks significantly increased the network’s training speed.
Result
Based on experiments with the MNIST and the ImageNet datasets, it can be concluded that the batch-normalized neural networks are much more robust, have higher accuracy, and train at a faster rate.
Conclusion
Batch normalization standardizes the inputs to a network and is applied to the prior layer activations. This reduces the impact of internal covariate shifts and aids in increasing training speed. It does, however, have some limitations. It is difficult to implement in the case of a Recurrent Neural Network and is also unsuitable for online learning. Though overall time decreases, per iteration time increases, and with larger batches, it increases even more.
The original authors believed it helped to reduce the problem of internal covariate shift. Some researchers have recently argued that batch normalization does not reduce internal covariate shift, but rather smooths the objective function, which improves performance. While the effect of batch normalization is noticeable, the reasons for its effectiveness are still being discussed. Nonetheless, it is widely used because it accelerates training and has numerous advantages.
